题目描述

一个链表中包含环，请找出该链表的环的入口结点。

【转】牛客网

方法一：

 

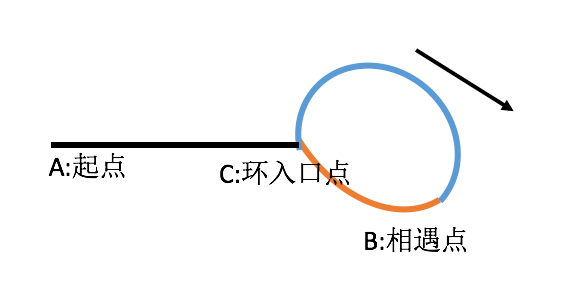
假设x为环前面的路程（黑色路程），a为环入口到相遇点的路程（蓝色路程，假设顺时针走）， c为环的长度（蓝色+橙色路程）

当快慢指针相遇的时候：

此时慢指针走的路程为Sslow = x + m * c + a

快指针走的路程为Sfast = x + n * c + a

2 Sslow = Sfast

2 * ( x + m*c + a ) = (x + n *c + a)

从而可以推导出：

x = (n - 2 * m )*c - a

= (n - 2 *m -1 )*c + c - a

即环前面的路程 = 数个环的长度（为可能为0） + c - a

什么是c - a？这是相遇点后，环后面部分的路程。（橙色路程）

所以，我们可以让一个指针从起点A开始走，让一个指针从相遇点B开始继续往后走，

2个指针速度一样，那么，当从原点的指针走到环入口点的时候（此时刚好走了x）

从相遇点开始走的那个指针也一定刚好到达环入口点。

所以2者会相遇，且恰好相遇在环的入口点。

最后，判断是否有环，且找环的算法复杂度为：

时间复杂度：O(n)

空间复杂度：O(1)

代码：

ListNode* EntryNodeOfLoop(ListNode* pHead)    {        if(pHead == NULL||pHead->next == NULL||pHead->next->next == NULL)            return NULL;        ListNode* tmp1 = pHead->next;        ListNode* tmp2 = pHead->next->next;        while(tmp1 != tmp2)        {            if(tmp2->next != NULL || tmp2->next->next == NULL)            {                tmp1 = tmp1->next;                tmp2 = tmp2->next->next;            }            else               return NULL;        }//相遇点        tmp1 = pHead;        while(tmp1 != tmp2)        {            tmp1 = tmp1->next;            tmp2 = tmp2->next;        }        return tmp1;    }

 

方法二：断链法

遍历一遍并将链的next置空，这样链中就不存在环了。

直到遍历到最后的节点就是环的入口节点。

由于要判断next节点，所以需要两个节点，其中一个节点记录上一节点。

代码：

publicListNode EntryNodeOfLoop(ListNode pHead){ if(pHead==null|| pHead.next==null)returnnull;     ListNode fast=pHead.next;     ListNode slow=pHead;     while(fast!=null){         slow.next=null;         slow=fast;         fast=fast.next;     }     returnslow; }